🇺🇸 Open Letter to Daron Acemoglu – On the Mathematical Thresholds of Civilizational Transitions 📜

A provocation on hunter-gatherers, Nash equilibria, and the limits of formal models in capturing the "golden blossom" of human agency

Dear Professor Acemoglu, 

 As a devotee of your work on institutional economics, I’ve long wondered: How would you formalize the precise moment when hunter-gatherers transitioned to agriculture? Not the aggregate effects (which your models brilliantly capture), but the mathematical singularity of the first human who chose to plant rather than forage—despite inferior short-term payoffs. 

Consider this thought experiment: 

1. The Nash Equilibrium Trap 

   Your work on extractive vs. inclusive institutions assumes rational actors. Yet the agricultural transition defies game theory: 

• Hunter-Gatherer Payoff Matrix: Foraging dominates planting (higher kcal/hr return for millennia). 
• The Anomaly: Some planted anyway. Why? 

2. A Missing Variable 

Could the "seed-planter’s dilemma" be modeled by adding: 

• φ (phi) = A non-utilitarian parameter (curiosity? ritual? sheer irrational hope?). 
• Where φ > ΔUtility for some critical threshold of actors. 

3. The Phase Transition 

Your Institutional Change framework could be enriched by treating φ as:

• Exogenous at first (random mutations? climate shocks?). 👉 Link
• Endogenous later (cultural selection via group survival). 

My Provocation: 

Mathematics stumbles when human choices cease to be computable—not due to complexity, but because the act of planting that first seed was a qualitative leap, akin to quantum superposition. The moment before planting, the payoff was undefined. 

Perhaps this is why all growth models (even yours) are post-hoc: They describe the diffusion of innovations, but not the origin—the irrational, "Golden Blossom" moment when a Nash equilibrium was first defied. 

I’d love to hear your thoughts. (And if this intrigues, I’ve drafted a follow-up on how φ might apply to today’s AI transition—where again, we’re blind to the "planters". 😉) 

With admiration, 

Hans 

"All great economic transitions begin where mathematics ends—and where a human, for reasons no model can contain, plants what others won’t." 

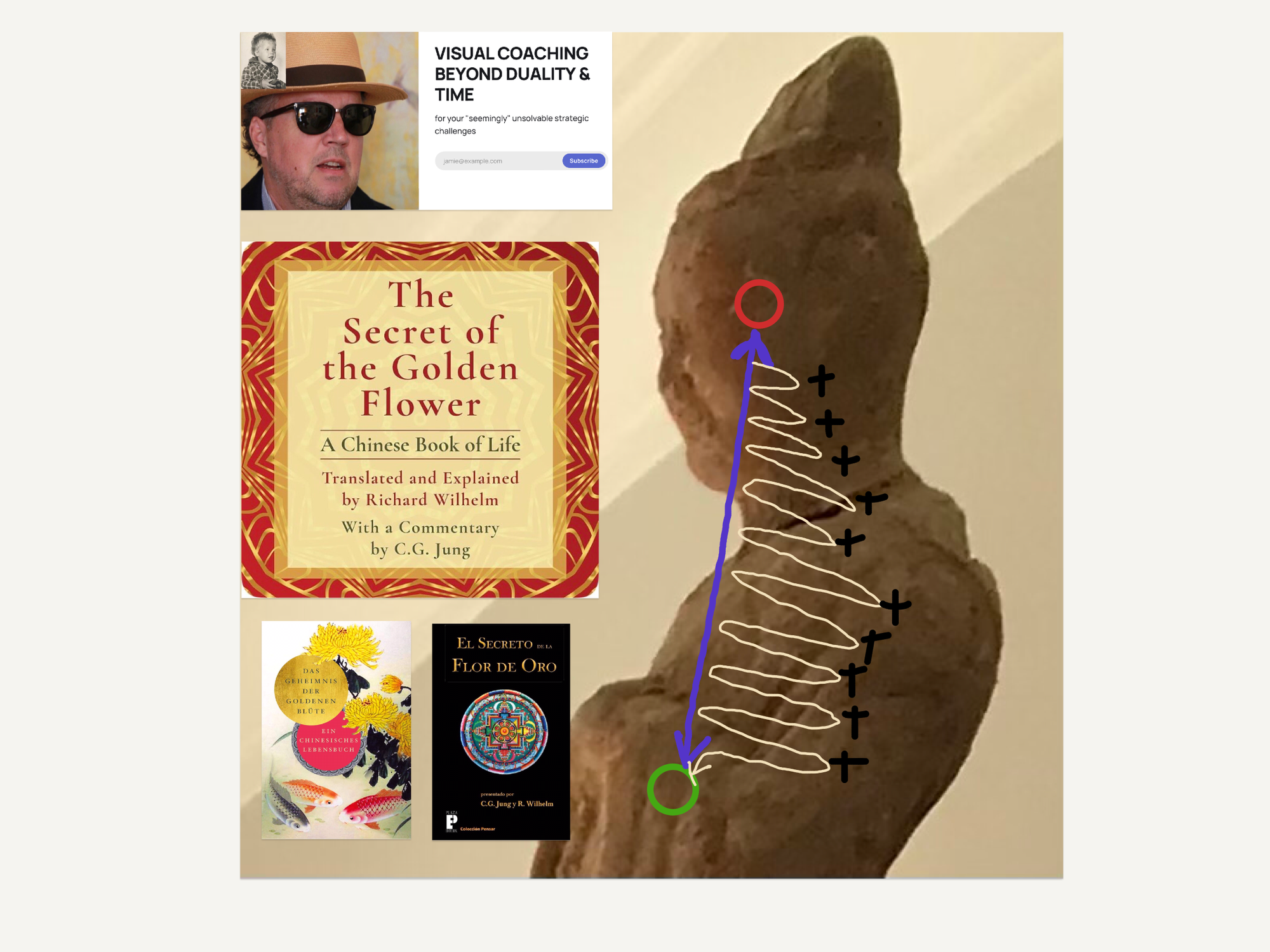
This post is the result of an inner image and a dialectical exchange between Hansjörg and an AI (=> for reference purposes only). I describe what I see inside myself – the AI reflects it back – the image changes – and thus a dance beyond the mind emerges.

In the end, everything comes together harmoniously, like a golden flower on a calm body of water.

I am merely a medium. The real work takes place within Hans. More about this process → [Link]

If these inspirations have touched you, I invite you to support the Golden Flower's mission: 

• With just 3,17 € per month (less than a cup of coffee), you can help spread this teaching around the world: [Membership link]
• Every donation goes towards posts, free offers and dialogue between tradition and modernity.
• Make a one-time donation here: [Donation link] – or share this post so that the seeds can be spread further.

Those who give, receive. Those who receive, give. The Golden Flower blooms in giving – but it is rooted in clarity. 🪷

As a "visual translator" between the quantum field and everyday reality (see Harvard bestseller 👉Link), I channel these images without conscious control – they flow through, not from me (👉Link). Every contribution keeps this bridge open: For your journey, for the next generation, for the undivided whole. Give only what feels light and joyful – the universe handles the rest.

👉 🇬🇧 Join my monthly Zoom session: "Ask My Self”🪷💫

⬆️ The result of "Inner Alchemy" (inner intuitive resonance & alignment with the quantum field): Me – on the left, aged 49, in my darkest hour in 2015, and on the right, today, aged 59 🪷💫